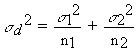Analysis of variance (ANOVA) for comparing means of three or more variables.

Use this test for comparing means of 3 or more samples/treatments, to avoid the error inherent in performing multiple t-tests

Background. If we have, say, 3 treatments to compare (A, B, C) then we would need 3 separate t-tests (comparing A with B, A with C, and B with C). If we had seven treatments we would need 21 separate t-tests. This would be time-consuming but, more important, it would be inherently flawed because in each t-test we accept a 5% chance of our conclusion being wrong (when we test for p = 0.05). So, in 21 tests we would expect (by probability) that one test would give us a false result. ANalysis Of Variance (ANOVA) overcomes this problem by enabling us to detect significant differences between the treatments as a whole. We do a single test to see if there are differences between the means at our chosen probability level.

Ideally, for this test we would have the same number of replicates for each treatment, but this is not essential. Advanced computer programmes can overcome the problem of unequal replicates by entering "missing values".

An important assumption underlies the Analysis of Variance: that all treatments have similar variance. If there are strong reasons to doubt this then the data might need to be transformed before the test can be done. In practice, there is a simple way to check for "homogeneity of variance". We deal with this at step "3" in the procedure below.

Procedure (see worked example)

Don't be frightened by this! It looks complicated but it is actually very easy. You should understand it, and then you can use a simple statistical programme (e.g. Microsoft "Excel") to run the whole test.

Assume that we have recorded the biomass of 3 bacteria in flasks of glucose broth, and we used 3 replicate flasks for each bacterium. [But the test could apply equally to any sort of variable]

Step 1. Record the data in columns:

Step 2. For each column, enter S x, n, , S x², and Sd² (click here for method)

Step 3. [A check for equal variance - the underlying assumption of this test] For each column divide Sd² by n-1 to obtain the variance, s ². Divide the highest value of s² by the lowest value of s ² to obtain a variance ratio (F). Then look up a table of F_max for the number of treatments in our table of data and the degrees of freedom (number of replicates per treatment -1). If our variance ratio does not exceed the F_max value then we are safe to proceed. If not, the data might need to be transformed.

Step 4. Sum all the values of S x² and call the sum A.

Step 5. Sum all the values for and call the sum B.

Step 6. Sum all the values for S x to obtain the grand total.

Step 7. Square the grand total and divide it by total number of observations; call this D.

Step 8. Calculate the Total sum of squares (S of S) = A - D

Step 9. Calculate the Between-treatments sum of squares = B - D

Step 10. Calculate the Residual sum of squares = A - B [This is sometimes called the Error sum of squares]

Step 11. Construct a table as follows, where *** represents items to be inserted, and where u = number of treatments and v = number of replicates.

[The total df is always one fewer than the total number of data entries]

Step 12. Using the mean squares in the final column of this table, do a variance ratio test to obtain an F value:

F = Between treatments mean square / Residual mean square

Step 13. Go to a table of F (p = 0.05) and read off the value where n₁ is the df of the between treatments mean square and n₂ is df of the residual mean square. If the calculated F value exceeds the tabulated value there is significant difference between treatments. If so, then look at the tabulated F values for p = 0.01 and then 0.001, to see if the treatment differences are more highly significant.

What does all this mean?

If you look at many of the steps above they should remind you of the steps in a t-test. For example, in a t-test we calculate S x, S x², and Sd² (which is the sum of squares), then we divide Sd² by n-1, just as we did in step 11 (above). So, the Analysis of Variance is using the same types of procedure, but for more than 2 samples. If you want to convince yourself of this, then try doing the Analysis of Variance for just two samples (e.g. Bacterium A and Bacterium B). You will get exactly the same result as in a t-test.

Analysis of variance: worked example

Replicate	Bacterium A	Bacterium B	Bacterium C	Row totals
1	12	20	40	72
2	15	19	35	69
3	9	23	42	74
S x	36	62	117	215 (Grand total)
n	3	3	3
	12	20.7	39
S x2	450	1290	4589	6329 (call this A)
	432	1281.3	4563	6276.3(call this B)
Sd2	18	8.7	26	52.7 (A - B)
s 2 (=Sd2 /n-1)	9.4	35	13

F_max test: F = 13/4.35 = 2.99. This is lower than the F_max of 87.5 (for 3 treatments and 2 df, at p = 0.05) so the variances are homogeneous and we can proceed with analysis of variance. If our value exceeded the tabulated F_max then we would need to transform the data.

D = (Grand total)² total observations = 2152 9 = 5136.1

Total sum of squares (S of S) = A - D = 1192.9

Between-treatments S of S = B - D = 1140.2

Residual S of S = A - B = 52.7

Source of variance	Sum of squares (S of S)	Degrees of freedom *	Mean square (= S of S df)
Between treatments	1140.2	u - 1 (=2)*	570.1
Residual	52.7	u(v-1) (=6)*	8.78
Total	1192.9	(uv)-1 (=8)*

[* For u treatments (3 in our case) and v replicates (3 in our case); the total df is one fewer than the total number of data values in the table (9 values in our case)]

F = Between treatments mean square /Residual mean square = 570.1 / 8.78 = 64.93

The tabulated value of F (p = 0.05) where u is df of between treatments mean square (2) and v is df of residual mean square (6) is 5.1. Our calculated F value exceeds this and even exceeds the tabulated F value for p = 0.001 (F = 27.0). So there is a very highly significant difference between treatments.

[Note that the term "mean square" in an Analysis of Variance is actually a variance - it is calculated by dividing the sum of squares by the degrees of freedom. In a t-test we would call it s ², obtained by dividing Sd² by n-1. Analysis of Variance involves the partitioning of the total variance into (1) variance associated with the different treatments/samples and (2) random variance, evidenced by the variability within the treatments. When we calculate the F value, we ask, in effect, "is there a large amount of variance associated with the different treatments compared with the amount of random variance?".]

Which treatments differ from one another?

The Analysis of Variance has told us only that there are differences between treatments in the experiment as a whole. Sometimes this information is useful in its own right. But it does not tell us which treatments differ from one another.

We now have a problem, because every time we compare one treatment with another (for example, comparing bacterium A with bacterium B) we are doing the equivalent of a t-test, with a probability of making a wrong interpretation. We need some way of avoiding this problem.

Method 1. Calculate the least significant difference between any two means. [This is not generally favoured, but it can be used with caution.]

We make use of the fact that our calculations for Analysis of Variance were similar to those of a t-test (see earlier); in particular, the residual mean square is an estimate of s² for each treatment, because the variance for all treatments is assumed to be equal in an Analysis of Variance.

In the t-test, we calculate s_d² as follows:

In the analysis of variance, s² for each treatment is assumed to be the same, and if n for each treatment is the same, then we could compare any two means by calculating s_d² as follows:

s_d² = 2 x residual mean square / n

We can then find s_d as the square root of s_d² and calculate t as:

If we did this for two particular means,we could compare the calculated t with that in a t-table, using the df of the residual mean square (because this reflects the residual variance in the whole experiment).

There is a simpler way of doing this for any two means:

If we take the equation and multiply each side by s_d we get: t (s_d) = ₁ - ₂

In other words, any two means would be significantly different from one another if they differ by more than "t multiplied by s_d"

So t(s_d) represents the least significant difference (LSD) between any two means.

In scientific papers you might see data presented as follows:

Here the author would be giving us the means for the 3 treatments (bacteria) and telling us that analysis of variance was used to find the least significant difference between any of the means at p = 0.05 (the level of probability chosen for the t value).

In fact, the table above uses the data for bacterial biomass in our worked example.

For 5% LSD, we find s_d² (= 2 x residual mean square / n). It is 17.56 /3 = 5.85.

We square root this to find s_d = 2.42.

The tabulated value of t for 6 df (of the residual mean square) is 2.45 (p = 0.05).

So the 5% LSD is t(s_d ) = 2.45 x 2.42 = 5.92.

Our table of data indicates that each bacterium produced a significantly different biomass from every other one.

A word of caution: We can be much more confident about significant difference between bacteria 1 and 3 or between bacteria 2 and 3 than we can about the difference between bacteria 1 and 2. Remember that every time we make such a comparison we run the risk of 5% error. But if we had used the t value for p = 0.01 then we could more safely make five comparisons and still have only a 1 in 20 chance of being wrong.

Statisticians recommend that the LSD should never be used indiscriminately, but only to test comparisons between treatments that we "nominated" when designing the experiment. For example, each treatment might be compared with a control, but each treatment should not necessarily be compared with each other treatment.

Method 2. Many people now use variants of the LSD, such as a Multiple Range Test, which enables us more safely to compare any treatments in a table. This test is far preferable to the LSD. It is explained separately on another page.

Analysis of variance: using "Excel"

The example that we used (bacterial biomass) above is shown below as a print-out from "Excel".

Having entered the data on the spreadsheet, we select Anova: single factor from the analysis tools, click OK, and enter all 9 cells of data in Input variable range. The table shows the source of variance as "Between groups" (= between treatments) and "within groups" (= residual). We are also told the calculated F value (64.949..), the F value that we would need to exceed (F critical) in order to have a significant difference between treatments, and the probability (p-value) that our calculated F value would be obtained by chance (random error) alone. This probability is very small (8.61 x 10^-5) so we have a highly significant difference between treatments in our table. We could then use the residual (within groups) mean square (MS) to calculate LSD, as explained earlier.

Note: There is always a danger in using a statistical package, because the package does whatever we tell it to do. It does not "think" or "consider" whether what we ask it to do is legitimate. For example, it does not test for homogeneity of variance. BEWARE!