This page covers four things: After reading this section, you should be able to decribe the main stages involved in scientific problem-solving. What is THE SCIENTIFIC METHOD? Science is usually fun. Most scientists enjoy their work, and fortunately it is sometimes useful to society. Since scientists are people rather than machines, they behave as other people do. They can be bad-tempered, pig-headed, jealous of the success of others and untruthful. Even so, the pattern of work employed by scientists, the scientific method, is the most powerful tool yet devised for the analysis and solution of problems in the natural world. The method can be applied as much to situations in everyday life as to conventional 'scientific' problems. The world might even be a happier place if more people attempted to solve their problems in a 'scientific' way. Scientific problem-solving has a number of recognisable stages:
Originality Science depends upon original thinking at several points. One is when we make the original 'guess' - usually called an hypothesis. Another is when we devise a test or experiment to show how likely the hypothesis is to be correct. A good scientist relies on 'inspiration' in the same way as a good artist. [Some teachers are concerned that this point is largely ignored in present-day science education.] THE SCIENTIFIC METHOD in practice - two everyday examples The examples constitute the sort of story you might read in a newspaper. We will try to analyse these stories in terms of THE SCIENTIFIC METHOD. A general feature is the lack of a rigorous test situation in the original stories; the strength of THE SCIENTIFIC METHOD largely lies in devising tests that are capable of discriminating between different hypotheses. 1. The dog that understands French Mr Smith of Morningside has taught his dog Rover to understand French. Mr Smith noticed that every evening, after dinner, when he went to the door with his coat on and said "Walkies", Rover immediately understood and came running. Mr Smith was going to France for the summer, and, as an experiment in international understanding, decided to teach Rover French. He started to say "Allons" instead of "Walkies". To his delight, Rover very quickly understood and came running. Analysis
The results of these and similar tests should indicate whether Rover is specifically responding to the word "allons", or (more likely) to an overall situation he is well used to. Notice that these tests do not tell us anything of a dog's ability to learn French words. They are only concerned with the specific case of responding to one French word. We will see later that extrapolating from the specific to the general is very important in scientific methodology. 2. Long-term success of a foreteller of the future The Institute for Psychical Research conducted a study on the performance of well-known fortune-tellers. The most positive results involve Arnold Woodchuck who, at the start of each year, makes a series of ten predictions for the coming year in a national tabloid newspaper. The Institute has found that Mr Woodchuck is consistently correct in about 80% of his predictions. For example, for 1995 he predicted a political crisis in Europe (the former Yugoslavia?), a major human disaster in Africa (Rwanda?), a dispute over public sector pay (nurses?) and the demise of a prominent football manager (Mr Graham?). He was unfortunately wrong in predicting that England would win the Rugby Union World Cup. A spokesman for the Institute was 'optimistic' about future studies on Mr Woodchuck. Analysis The apparent observation is that Mr Woodchuck has got more predictions correct than would have been expected by chance. The Institute's hypothesis would be that Mr Woodchuck has some kind of 'psychic powers'. Can we devise an alternative hypothesis? We are dealing here with probability. If we toss an unbiassed coin we get on average the same number of heads as tails. If we asked someone to predict the outcome of the toss, we would not be terribly surprised if from a small number of trials, he got 4 out of 5 right. But if he continued to achieve 80% success over a long series, we would begin to suspect: (1) a biased coin; (2) cheating; (3) psychic powers. Mr Woodchuck regularly gets 80%. Is his 'coin' biased, is he cheating, or does he have psychic powers? The most likely explanation is the 'biased coin' one, i.e. that the events he predicts do not have a 1:1 probability, but perhaps a probability nearer to 4 or 5:1 on; in other words, a very high probability that they will occur. We have therefore two kinds of test:
For example, almost invariably every year there is at least one 'political crisis' in Europe and a 'major human disaster' in Africa. Similarly, football managers have a short shelf-life. Public sector employees (such as nurses, railway signalmen or indeed University teachers) have for years perceived themselves to be underpaid whilst their masters either cannot or will not respond appropriately. In contrast, the chances of England's winning the Rugby Union World Cup were over-stated by the English press - and this is a prediction that failed.
Again, the results of this investigation would be limited. They would probably show that the 'biased coin' explanation is the most likely. They would not show (a) whether Mr Woodchuck has some kind of psychic power; or (b) whether psychic powers are possible. Notice also that even a large deviation from an expected result can occur by chance in a small sample (e.g., getting 4 out of 5 coin-tossing guesses right). This is very important in Biology, and the basis of the use of statistical methods in biological analysis. After reading this section you should be able to discriminate between good and bad experimental design. Experimental Design The design of a suitable experiment to test an hypothesis often requires some ingenuity and a suspicious nature. In modern biology, the experiment may involve very sophisticated equipment. But there are a number of features common to all good experiments (and often absent from bad ones) which exist whatever the technical details. In summary these are: Discrimination Experiments should be capable of discriminating clearly between different hypotheses. It often turns out that two or more hypotheses give indistinguishable results when tested by poorly-designed experiments. Replication and generality Living material is notoriously variable. Usually experiments must be repeated enough times for the results to be analysed statistically. Similarly, because of biological variability, we must be cautious of generalising our results either from individual creatures to others of the same species, or to other species. For instance, if our hypothesis is about mammals, it is inadequate simply to carry out our experiments on laboratory rats. Similarly, it is dangerous to extrapolate from healthy students to elite athletes. Controls The experiment must be well controlled. We must eliminate by proper checks the possibility that other factors in the overall test situation produce the effect we are observing, rather than the factor we are interested in. An example: Growth hormone is secreted in response to a number of agents, including the amino acid arginine. This was shown by injecting volunteers with arginine. As a control, the investigators injected the volunteers with a saline solution. To their surprise, growth hormone was again secreted. The investigators then waved a syringe and needle in front of their volunteers, and found that that provoked growth hormone secretion too. Growth hormone is now known to be secreted in response to stress (as well as arginine). At a more technical level, we must be sure that our method of measurement is reproducible from day to day, between operators in the same laboratory, or between laboratories. Whilst we might be confident about a balance or a ruler, can we be as sure about, say, a method for measuring haemoglobin? Do two groups of students measuring the same samples by the same methods produce the same results? Quality control helps here. 'Blind' Designs Investigators can subconsciously 'fudge' their data if they know what result they want to find. The answer is to do the experiment 'blind', so the investigators (and the subjects, if humans are being studied) do not know which treatment's effect they are observing. This can make the logistics of doing the experiment more complex: for example, when determining the haemoglobin concentration of male and female class members. There is a story about a professor who devised a maze for measuring the intelligence of rats. One day he gave his technicians, who actually made the measurements, three groups of rats. He told them one group had been specially bred for intelligence, one for stupidity and the third was average. The technicians assessed the rats' intelligence and confirmed that the 'bright' group performed the best and the 'stupid' group the worst. The point is, of course, that the professor had put animals into the three groups at random. They did not differ in intelligence. Measurement Good experiments often, though not always, involve measuring something: a weight, say. When you make measurements, it is important you know both the accuracy and the precision of your measuring system. These two terms are not synonymous: 'accuracy' means the ability of the method to give an unbiassed answer on average, whereas 'precision' is an index of the method's reproducibility. Ideally your method should be both accurate (i.e., give the true mean) and precise (i.e., have a low standard deviation). Sometimes one is more important than the other. For example, if you were looking for small changes with time in a quantity (such as an athlete's haemoglobin concentration), you would need a precise measure of it rather more than an accurate one. Accuracy and precision together help you to judge the reliability of your data. They also help you to judge to how many significant figures you should quote your results. For example, if you use a balance reading to the nearest gram, you should give the results to the nearest gram and not, say, to the nearest tenth of a gram. Some experiments are very difficult to do because it is not obvious what can be measured. This is a real problem in animal behaviour: for example, there is no obvious unit or measure for 'emotional state'. It is usually necessary to isolate measurable components of behaviour. Thus the speed at which a tiger paces up and down a cage can give some indication of the internal state of the animal but can never give a full picture of it. Many of these points are rather abstract, but they should become clearer when you think about the following examples. Example 1: Do plants give off water vapour? Experiment: Forty bean plants, growing in pots, were covered one afternoon by individual glass containers and left in the laboratory overnight. Next morning, the inside of the lid of each container was found to be covered in droplets of a fluid which proved to be water. Conclusion: Plants generally give off water vapour. Critique 1. Lack of controls.
2. The conclusion contains some points that are not valid.
Example 2: Is your supermarket's 'own brand' of washing powder as good as a nationally-advertised one? Eric Triton bemoaned the fact that his wife Ariel insisted on washing his clothes with their local supermarket's own brand of powder. He was sure the well-known brand he saw performing miracles on television most evenings would do better. He therefore set out to prove as much. Mr Triton decided to compare the effectiveness of the two products on what his wife called 'difficult' dirt: grass stains on white linen handkerchiefs. He bought 4kg of the well-known brand for £5.17 in their supermarket and noted that the same weight of the own-brand powder would have cost £4.47. He followed the instructions on the packets exactly, weighing out the same amount of powder and using their washing machine's programme for white linens. Mr Triton was aware of the need for an index of 'cleanliness' and therefore devised a subjective scale, ranging from 10 ('whiter than white') to 0 (the starting level of dirtiness). Mr Triton's belief was substantially confirmed. He scored the handkerchief cleaned by the national brand an impressive 8, whereas the own-brand powder only managed 7. Triumphantly, he reported the outcome to his wife. Mrs Triton, however, was unimpressed. She pointed out to her husband that there were several flaws in his experiment and convinced him that the outcome was 'not proven'.
Further reading: Barnard C, Gilbert F and McGregor P (1993) Asking Questions in Biology, Longmans. DESIGNING EXPERIMENTS TO USE STATISTICS There is a story about an eminent Professor at Cambridge who gave a paper at a scientific meeting and was asked by a questioner "what statistical test did you use to verify your results?" The Professor explained that he used his own statistical test: "In our Department we have a long corridor with a notice board at one end. I draw a histogram of my results, pin it to the notice board, then walk to the other end of the corridor. If I can still see a difference between the treatments then it's significant" The relevance of this story lies in what it does not say! If an experiment is designed and executed properly - as we would expect of an eminent scientist - then the results often speak for themselves. For example, this might be true of experiments in which mutants are generated (or genes inserted) in an organism, giving a clear change of behaviour such as resistance to an antibiotic or expression of a new trait. Such "all or nothing" effects seldom need to be backed by statistical tests, but they still need good experimental design. However, in many areas of biology we work with variable effects - differences in the growth rates of organisms, quantitative differences in antibiotic resistance or in size or in rates of biochemical reactions, etc. Then we not only need statistical tests to analyse those differences but we also need good experimental design to ensure that we haven't biased our results in some way, without realising it. Good experimental design is the key to good science. But it's not as easy as it might seem. In many cases good experimental design involves having a clear idea about how we will analyse the results when we get them. That's why statisiticians often tell us to think about the statistical tests we will use before we start an experiment. Three important steps in good experimental design 1. Define the objectives. Record (i.e. write down) precisely what you want to test in an experiment. 2. Devise a strategy. Record precisely how you can achieve the objective. This includes thinking about the size and structure of the experiment - how many treatments? how many replicates? how will the results be analysed? 3. Set down all the operational details. How will the experiment be performed in practice? In what order will things be done? Should the treatments be randomised or follow a set structure? Can the experiment be done in a day? Will there be time for lunch? etc. If all this sounds trivial or obvious, then read on. It's not as easy as you think! Example 1. Experiments that yield no useful results because we did not collect enough data Suppose that we want to test the results of a Mendelian genetic cross. We start with 2 parents of genotype AABB and aabb (where A and a represent the dominant and recessive alleles of one gene, and B and b represent the dominant and recessive alleles of another gene). We know that all the F1 generation (first generation progeny of these parents) will have genotype AaBb and that their phenotype will display both dominant alleles (e.g. in fruit flies all the F1 generation will have red eyes rather than white eyes, and normal wings rather than stubby wings). This F1 generation will produce 4 types of gamete (AB, Ab, aB and ab), and when we self-cross the F1 generation we will end up with a variety of F2 genotypes (see the table below).
All these genotypes fall into 4 phenotypes, shown by colours in the table: double dominant, single dominant A, single dominant B and double recessive. And we know that in classical Mendelian genetics the ratio of these phenotypes is 9:3:3:1 Most people also know that we use a chi squared test to analyse the results of genetic crosses: we do our experiment, count the number of F2 progeny that fall into the different categories, and test to see if our results agree with an expectation. In this case, the expectation would be that the results fit a 9:3:3:1 ratio. But what you might not know is that a chi squared test would only be valid if every expected category in this case is 5 or more (it does not matter what the actual count is in each category, but the expected count must be 5 or more). In other words, we MUST have at least 80 F2 progeny in order to use the chi squared test for this experiment, because then the smallest category - double recessive - would have an expected 5 individuals in it (one-sixteenth of 80 being 5). [A fuller explanation of this is given in Chi squared test.] Similarly, for comparing two counts (e.g. counts from dilution plating of bacteria) by means of a Poisson distribution, you will need to count about 30 colonies at the chosen dilution level. [The principles underlying the Poisson distribution do not hold for counts lower than this] As a different example along the same lines, we might want to compare the biomass produced by plant callus culture in flasks containing different nutrient solutions. We know that we need more than one flask of each nutrient solution (i.e. we need replicates), and we will use Student's t-test to compare the mean growth in each solution. [Basically, a t-test compares the difference between the two means in relation to the amount of variation within the treatments. In other words, we get a significant result if the difference between the means is large and/or the variation between replicates is small]. So, how many replicates should we use? This is a matter of judgement (and the available resources) but if we look at a t-table we can make some rational decisions. If we use 2 flasks for each treatment (4 flasks in total), we would have 2 degrees of freedom. This term is explained elsewhere, but for now we can note that the number of degrees of freedom for each treatment is one less than the number of replicates. In other words, with 2 treatments of 2 flasks each we have 2 degrees of freedom. With 2 treatments of 10 flasks each we have 18 degrees of freedom. When we analyse our results by Student's t-test, we calculate a t value and compare it with the t value for probability of 0.05 in the t-table. Our treatments differ significantly if the calculated t value is greater than the tabulated value. Look at the tabulated t value (4.30) for 2 degrees of freedom. It is quite high, and we would only find a significant difference between our treatments if we have quite a large difference between the means and also little variation in our replicates. But if we used 4 replicates of each treatment (6 degrees of freedom) we would have a much better chance of finding a significant difference (t value of 2.45) between the same means. But look even further down the t-table - e.g. downwards from 10 degrees of freedom (t-value 2.23) - and we see that we would gain very little by using any more replicates. We would be in the realm of diminishing returns, gaining very little for all the extra time and resources. The message from these examples is that knowledge of the statistical test that we will use helps us to design our experiment properly. Example 2. Experiments that seem to give useful results but our procedures let us down! Under this heading we deal with the actual process of doing an experiment - a task with many hidden pitfalls. Suppose we decide to compare 4 treatments, with 4 replicates each - a total of 16 flasks of bacteria, 16 potted plants, 16 biochemical reactions to measure with a spectrophotometer, etc. We do the experiment, get nice results, analyse them (the appropriate test would be Analysis of Variance) and find significant differences between the treatments. We write up the results, get a Nobel Prize, or a good mark, or whatever. End of story. Or is it? The answer to that question depends on how we did the experiment. For example, there might have been a good "practical" (i.e. convenient) reason for setting up all replicates of treatment 1, then (for example) changing the pipette and setting up all replicates of treatment 2, and so on. The problem is: how can we be sure that the difference we found between treatments was due to the treatments themsleves, and was not influenced by the order in which we set them up? Even if we DO feel sure, our experiment is inherently biased and nobody would trust the results if we said how we did it! [There is an almost infinite number of reasons why the conditions might change during the time taken to set up an experiment. For example, we might get progressively more efficient, or more tired. The temperature of the water bath (or whatever) might change slightly during this time. Each pipette will be slightly different from the next, etc. etc.] So, what about doing one replicate of treatment 1, then one of treatment 2, then 3, then 4, and then doing a second replicate of treatment 1, a second of treatment 2, and so on? In truth, this would remove only some of the inherent bias - on average, treatment 1 is still being set up before treatment 2, etc. The only way to overcome this is to plan in advance. We have basically two options.
And one last point - the same principles should be applied to other practical aspects of an experiment. For example, have you ever tested the temperature gradient in a laboratory incubator or (worse still) in a walk-in growth room? The temperature gauge might record "30oC" but there is likely to be a vertical (or lateral) temperature gradient of 2-3o or more. So never put all the replicates of one treatment together. Randomise them. To block or not to block? For most experiments we would simply randomise the treatments and replicates. There is an important statistical reason for this, because all the statistical procedures are based on the fundamental assumption that variation is random: in other words, that it is determined by chance alone. But "blocking" becomes useful, or even essential, if we know (or strongly suspect) that "extraneous" factors will introduce variation that is irrelevant to the effects we wish to test and that might mask the effects of our treatments. Here are two examples, and you could think of many more along the same lines.
Suppose that we are measuring the size of cells, the height of trees, the biomass of microbial cultures, the number of eggs in nests, or anything else. The thing that we are measuring or recording (e.g. cell size, plant height, etc.) is called a variable. Each measurement that we record (e.g. the size of each cell) is a value or observation. We obtain a number of values (e.g. 100 for cells), and this is our sample. The sample (e.g. 100 cells) is part of a population. In this case the population (in biological terms) is all the cells in the culture (or all the trees in a forest, etc.). Theoretically, we could measure every cell or tree to get a precise measure of that population. But often we want to be able to say more than this - something of general significance, based on our sample. For example, that if anyone were to measure the cells of that organism, then they would find a certain average value and a certain range of variation. Here are 3 sorts of thing that you might want to say.
General statements such as these will always be based on a sample, because we could never test every possible strain of E. coli, nor measure every possible adult, nor test every possible rat that could ever live. So, in these and in many other cases the population can be considered to be infinite. That's the sense in which statisticians use the term "population" - for all the possible measurements or events (i.e. all the possible values of a variable) of a particular type that there could ever be. In statistics, we use SAMPLES to ESTIMATE the PARAMETERS of a POPULATION. The statistical procedures are based on quite complex mathematics. But that need not concern us at all, because the procedures are actually very simple to apply. Basically, from our sample we calculate:
Having obtained those values, we use them to estimate
the population mean and the population
variance. In order to distringuish between what
we measure (samples) and what we wish to estimate
(populations) from the samples, many statisticians use
greek letters for the population mean
(which is denoted m
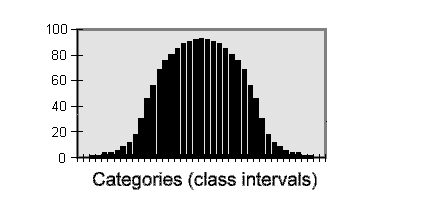
(mu) instead of We cover these points under Descriptive statistics. But before we move on to that, we must consider briefly how variation is distributed in statistical terms. If we measured cells or people or plants or biochemical reactions (as absorbance values in a spectrophotometer) etc. we would find a range of variation. As we made more and more measurements of this type they would display a continuous range of variation. If we were to put these measurements into appropriate categories or class intervals (for example, all the measurements that fall between 1.0 and less than 2.0, all between 2.0 and less than 3.0, and so on) and then plot the numbers in each category as a histogram it would look like this:
Given enough measurements (and small enough class intervals), this would be a completely symmetrical, bell-shaped curve. Data of this sort are said to be normally distributed. Most of our measurements (data points) would be close to the mean, and progressively fewer would depart widely from the mean. Most of the statistical tests that we consider on this site are for normally distributed data. But there are other types of distribution. For example, if we measured the heights of men and women as a single population they might form a bimodal distribution - two humps with a dip between them, because women, on average, are shorter than men. Then we should treat them as two populations, not as a single one. Other types of data, such as counts, fall naturally into "either/or" categories. These are treated in different ways, some of which are explained later. Before applying a statistical test, the experimenter must check what sort of distribution applies to the data. Often, logic, simple observation, and past experience are enough for this. |
||||||||||||||||||||||||||||||||||||||||||||||||||