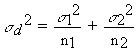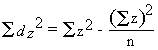Paired-samples test

Use this test as an alternative to the t-test, for cases where data can be paired to reduce incidental variation - i.e. variation that you expect to be present but that is irrelevant to the hypothesis you want to test.

As background, let us consider exactly what we do in a conventional t-test to compare two samples. We compare the size of the difference between two means in relation to the amount of inherent variability (the random error, not related to treatment differences) in the data. If the random error is large then we are unlikely to find a significant difference between means unless this difference is also very large.

Consider the data in the table below, which shows the number of years' remission from symptoms (of cancer, AIDS, etc.) in two groups of patients: group A who received a new drug and group B who received a placebo (the controls). There were10 patients in each group, and we will first analyse the data by conventional t-test (see Student's t-test if you are not familiar with this).

Patient	Drug	Placebo
1	7	4
2	5	3
3	2	1
4	8	6
5	3	2
6	4	4
7	10	9
8	7	5
9	4	3
10	9	8
S x	59	45
n	10	10
	5.9	4.5
S x2	413	261
(S x)2 / n	348	203
	65	58
s 2	7.22	6.44
		= 1.37
sd	= 1.17
	= 0.67

Clearly, there is no significant difference between the means. [The smallest tabulated t value for significant difference at p = 0.05 is 1.96.]

But drug trials are never done as randomly as this. Instead, the patients are matched as nearly as possible to exclude the effects of extraneous variation. For example, patient 1 in each group (drug or placebo) might be a Caucasian male aged 20-25; patient 2 in each group might be an Asian female aged 40-50, and so on. There is every reason to suspect that age, sex, social factors etc. could influence the course of a disease, and it would be foolish not to exclude this variation if the purpose of the trial is to see if the drug actually has an overall effect. In other words, we are not dealing with random groups but with purposefully paired observations. (The same would be true if, for example, we wanted to test effects of a fungicide against a disease on 10 farms, or to test whether a range of different bacteria are sensitive to an antibiotic, etc.).

Now we will analyse the data as paired samples.

Procedure (see worked example later)

1. Subtract each control value from the corresponding treatment value and call the difference z. (NB Always subtract in the same "direction", recording negative values where they occur)

2. Calculate S z, , S z² and (S z)² /n , where "n" is the number of pairs (z values)

3. Construct a null hypothesis. In this case it would be appropriate to "expect" no difference between the groups (drug treatment versus controls). If this were true then the observed values of z would have a mean close to zero, with variation about this mean.

4. Calculate:

5. Calculate:

6. Square root this to find s_d then calculate:

7. Find t from the equation:

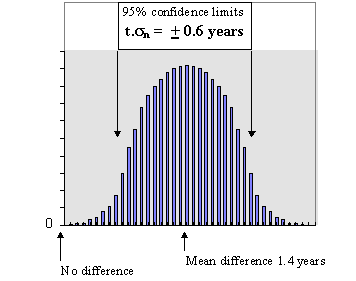
8. Consult a t table at n-1 degrees of freedom, where n is the number of pairs (number of z values). The tabulated t value for 9 df is 2.26 (p = 0.05)

In our example the calculated t value is 5.24, which is very highly significant - it exceeds the t value for probability (p) of 0.001. In other words, we would expect such a result to occur by chance only once in a thousand times. So the drug is effective: we see below that it gives remissison of symptoms for 1.4 0.266 years (this value is the mean standard error of the mean). The confidence limits are 1.4 0.6 years (mean t.s_n).

Patient	Drug	Placebo	Difference (z)
1	7	4	3
2	5	3	2
3	2	1	1
4	8	6	2
5	3	2	1
6	4	4	0
7	10	9	1
8	7	5	2
9	4	3	1
10	9	8	1
S z			14
n			10
			1.4
S z2			26
(S z)2 / n			19.6
			6.4
s d2			0.71
s d			0.84
s n			0.267

t = 1.4/0.267 = 5.24

It is instructive to consider what we have done in this analysis. We calculated the mean difference between the pairs of patients (treatments), calculated the standard error of this mean difference and tested it to see if it is significantly different from zero (no difference). The following diagram should make this clear.

Paired-samples t-test: print-out from "Excel".

The example above was run on "Excel", as before (see Student's t-test) but we select t-test: paired two sample for means from the analysis tools package, click OK, select the whole data set (cells B2-C11) for Input variable range and a clear cell for Output range. See Student's t-test for explanation of other relevant entries in the print-out. [The calculated t (5.25) differs slightly from the worked example (5.24) on the previous page because the computer did not round up the decimal points during calculations]

******** Note that the two-tailed t-test shows the drug and placebo to be significantly different at p = 0.0005 (probability of 5 in 10,000 that we would get this result by chance alone). But in this case we would be justified in using a one-tailed test (P = 0.00026) because we are testing whether the mean difference (1.4 years) is significantly greater than zero. Look at the ‘critical t’ for a one-tailed test in the printout. This is the value given forp = 0.1 in a t-table (because we are testing only for a difference in one direction - above zero - so we can double the normal probability of 0.05). We should have used this value, not the value for p = 0.05 in our testing for significance.