|
Sounds boring, but it's about giving the most - and most useful - information from a set of data. IMPORTANT: AN OVERVIEW OF THIS SECTION. When we take measurements or record data - for example, the height of people - we cannot possibly measure every person in the world (or, as another example, every cell of a particular type of bacterium). Instead, we have to take a representative sample, and from that sample we might wish to say something of wider significance - something about the population (e.g. all the people in the world, or all the bacteria of that type). So, we use samples as estimates of populations. But in many cases they can only be estimates, because if our sample size had been greater (or if we had measured a different sample) then our estimate would have been slightly different. Statistical techniques are based on probability, and enable us to make the jump from samples to populations. But we should never lose sight of the fact that our initial sample can only be an estimate of a population. In the following sections we will start from a small sample, describe it in statistical terms, and then use it to derive estimates of a population. ______________________________________ A sample Here are some values of a variable: 120, 135, 160, 150. We will assume that they are measurements of the diameter of 4 cells, but they could be the mass of 4 cultures, the lethal dose of a drug in 4 experiments with different batches of experimental animals, the heights of 4 plants, or anything else. Each value is a replicate - a repeat of a measurement of the variable. In statistical terms, these data represent our sample. We want to summarize these data in the most meaningful way. So, we need to state:
Now we will go through these points, explaining the meaning of the procedures. If you are familiar with all this, you can go straight to Describing a population: practical steps. How to express the variability of data as variance or standard deviation The sample variance (S2) There is a simple formula for calculating the variance of the sample (S2). It is given below, but first we should see how it is derived. Each data point (measurement) in our sample differs from the mean by an amount called the deviation (d). We could, in theory, find each d value by subtraction (keeping the sign as + or -), then square each deviation, add all the d 2 values (to get the sum of squares of the deviations, shortened to the sum of squares) and divide this by n-1 to give the variance, where n is the number of observations in our sample. We can then obtain the standard deviation (notation, S), which is the square root of the variance. Why do we use n-1 and not n? You should just accept this as standard and necessary practice! However, it has a reason, based on the fact that we almost always use the sample variance to obtain an estimate of the population variance (a population being all the measurements or events of the same type that could ever be found). Put in simple terms, the population variance is derived from the sample mean and from the deviation (d) of each measurement from the sample mean. But if we lacked any one of these measurements (the mean or a single d value) we could calculate it from the other information. So, with n measurements (data points) only n-1 of them are free to vary when we know the mean - we could calculate the missing one. "n-1" is therefore the number of degrees of freedom of our data. The formula for calculating Sample variance For each observation (x) the deviation (d)
from the mean ( Therefore d2
= (x - Expanding this equation, we get: d2
= x2 - 2x. To obtain the sum of squares of the deviations, we sum both sides of this equation (the capital letter sigma, S = sum of): Sd2 = Sx2 - 2Sx From this equation we can derive the following important equation for the sum of squares, Sd2.
Then we find the sample variance and sample standard deviation: sample variance (S2)
= standard deviation (S)
= If we present the mean Now we can express our data as This is the conventional way in which you see data
published. For example, if the four values (120, 135,
160, 150) given earlier were the diameters of four cells,
measured in micrometres, then we would say that the mean
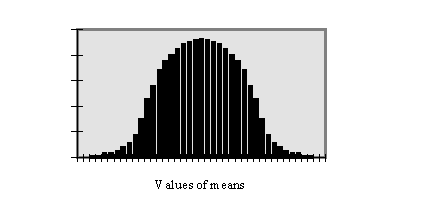
cell diameter was 138.8 Further steps: the standard error of a mean What we have done so far is useful, but not useful enough! If we think about it, we will see that the estimate of the population mean (i.e. all the measurements that we ever could make of the same type - the diameter of this type of cell, etc.) has been fixed by the sample of four individuals. If we did the experiment again by measuring another 4 cells then we almost certainly would get a different mean. What we really want to know is "how good is our estimate of the mean?", not "how much variation was found around this particular estimate of the mean?" We do this by calculating the standard error (standard deviation of the mean). Imagine that we repeat the experiment again and again, with a different set of cells (or other types of variable). Each time, we would get a slightly different mean, but if we were to plot a frequency distribution (histogram) of the means then it would show a normal distribution:
We could find the mean of the means and then calculate a standard deviation of it (not the standard deviation around a single mean). By convention, this standard deviation of the mean is called the standard error (SE) or standard error of the mean (SEM). The notation for the standard error of the mean is sn We do not need to repeat our experiment many times for this, because there is a simple statistical way of estimating sn which is based on: sn = s / Ö n. (For this we are using S as an estimate of s). So, if we had a sample of 4 values (120, 135, 160,
150) and the mean with standard deviation ( Note 1. You don't need to understand
the mathematics behind the use of Ö
n. Look on it as a "sliding scale"
that compensates for the number of values (data points)
in the original sample. Confidence intervals of a mean A calculated value for a standard deviation or a standard error has little practical use in itself. But it becomes meaningful when we use it to calculate confidence intervals.We can do this easily by multiplying a standard deviation or a standard error by a t value obtained from a table of t. The confidence intervals show us the range within which 95% or 99% or 99.9% of observations could be expected to lie. We will illustrate this with the 4 values that we mentioned above (120, 135, 160, 150). We found a mean with standard error of the mean (138.8
If we had measured an infinite number of cells we would consult the bottom line of a table of t values (Student's t-test), which appears as follows.
We select the level of confidence we
want (usually 95% in biological work - see the notes
below) and multiply s by the
tabulated value. If But our sample was not infinite - we had 4 measurements - so we use the t value corresponding to 4 measurements, not to ¥ . The t table shows degrees of freedom (df), which are always one less than the number of observations. For 4 observations there are 3 df, because if we knew any 3 values and we also knew the mean, then the fourth value would not be free to vary. To obtain a confidence interval, we multiply sn by a t
value as before, using the df in our original data.
In our example, the 95% confidence interval would be
138.8 When do we use the standard error? Many people prefer to cite the standard error rather than standard deviation, because it makes the range of variation appear to be smaller! But it has real value in telling us something - for example, that if anyone were to repeat our experiment, then the mean would be likely to fall within the limits of t x sn. Note the following points 1. The standard deviation is a measure of variability in our data and is an estimate of s, an important property of the population. 2. We choose the level of confidence we wish to place on our data. The confidence limits will be larger if we choose a higher level of confidence (e.g. 99% compared with 95%). However, for most biological work we use the 95% level. 3. The number of degrees of freedom determines the t value. So, when designing experiments we have to find a compromise between the level of confidence we want and the amount of work involved. Inspection of a t table shows that the values fall off rapidly from 2 to 5 df (3 to 6 replicate observations) but more slowly thereafter. [Note that a t-table does not have space to give us every degree of freedom, so if a sample has a degree of freedom that falls between two entries in a t-table (say between 60 and 120) then you should use the t value for 60 df in the table.] Describing a population: practical steps (see the worked example below) 1. Tabulate the data. 2. Sum the data to obtain S x, then square this to obtain (S x)2 3. Calculate the mean, 4. Square each data value and sum the squares to obtain S x2 5. Calculate 6. Estimate the variance of the population (s2) as:
7. Find the estimated standard deviation of the population (s ) = square root of the variance. 8. Calculate the estimated standard error (SE) of the mean (s n) = s / Ö n
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
) is x - 
standard deviation, we will have summarised in just
two numbers the most important properties of the sample
that we used. This also is our estimate of the
mean (m)
and standard deviation (sigma, s
) of the population. 